Study Guide 2: Graphics Fundamentals

Quizes are closed book. 30 minutes in lab.

Topics:

Everything from Study Guide 1 plus

  • Meshes and normals

  • Graphics pipeline

  • Shaders

  • Phong shading

  • Matrix stack

  • Particle systems

Please also use your lab worksheets as study resources.

Short Answers

Meshes and normals

  • What is a triangle mesh?

  • A well-formed mesh is a manifold? What properties does this imply?

  • If we wish to allow a manifold with boundaries, what properties apply?

  • What is triangle orientation and why is it important for meshes?

  • How do we store a triangle mesh using shared vertices?

  • What are surface normals? Why are they important for shading?

Graphics pipeline and shaders

  • The four primary stages of the graphics pipeline are the application, geometry processing, rasterization, and pixel processing. Briefly describe each step.

  • What operations happen during geometry processing?

  • During which stage of the graphics pipeline is the vertex shader called?

  • During which stage of the graphics pipeline is the fragment shader called?

  • During which stage of the graphics pipeline do we handle user input?

  • During which stage of the graphics pipeline do we perform blending when we need transparency?

  • What is camera (aka eye or view) space?

  • What is local (aka object or model) space?

  • What is world space?

  • What is the canonical view volume (CVV)?

  • Why do we project positions to the CVV as opposed to a 2D image?

  • What is clipping?

  • What is the depth, or Z buffer?

  • Why do transparent objects need to be rendered from back to front, with respect to the camera?

  • What types of operations does the graphics card compute in parallel?

Phong shading

  • What three colors do we compute as part of the phong shading model?

  • When rendering an object with phong shading, what uniform parameters do we need to specify to configure the material of an object?

  • The diffuse intensity is computed using which vectors at a point p?

  • The specular intensity is computed using which vectors at a point p?

  • What coordinate system do we use to compute shading?

  • What is the position of the camera in eye space?

  • Sketch how to implement phong shading in a vertex shader.

  • Sketch how to implement phong shading in a fragment shader.

  • Sketch how to implement a toon shader without an outline.

Textures

  • What is a texture?

  • What are the benefits of using textures?

  • What are texture coordinates? How do they relate to texturing meshes?

  • How can we handle cases where the texture coordinates do not range between 0 and 1?

Particles and billboards

  • What is a particle system?

  • What is an object pool?

  • Why might we use billboards to render particles?

  • What else might we render with billboards besides particle systems?

  • What is the difference between additive and alpha blending?

Sample questions

  • Which of the following meshes is a manifold? Why or why not?

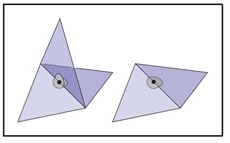
manifold ex1

  • Which of the following meshes is a manifold? Why or why not?

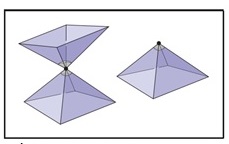
manifold ex2

  • Suppose we wish to store the following geometry using an indexed mesh (shared vertices) and triangle strip primitive. What would our position and index buffers contain?

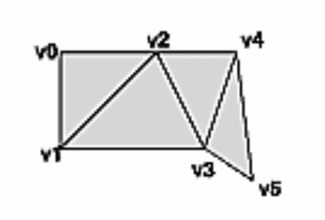
triangle strip ex1

  • Suppose we wish to store the following geometry using an indexed mesh (shared vertices) and triangle primitives. What would our position and index buffers contain?

triangle strip ex1

  • Suppose we have a triangle with corner points a, b, and c. What is the normal to the surface? Give a formula in terms of a, b, and c.

  • Sketch the code for a vertex shader which takes in positions in local coordinates and outputs gl_Position in projected coordinates. Be sure to include any uniform parameters you need as well as any buffer inputs.

  • Sketch the code for a fragment shader that colors all pixels green, e.g. (0,1,0).

  • Show how you would modify the following shader to animate the input position so it revolves around the origin.

#version 400

layout (location = 0) in vec3 vPos;
layout (location = 1) in vec3 vNormals;
layout (location = 2) in vec2 vTextureCoords;

uniform mat4 MVP;

void main()
{




   gl_Position = MVP * vec4(vPos, 1.0);
}

  • What is the normal to the XY plane?

  • Suppose we are visualizing normals in a fragment shader using the formula color = (normal + 1)*0.5. If the normal is (-1,0,0), what color do we expect to see?

  • On line 8 of the following program, what model tranform will be used to draw the cube? Assume that in local coordinates, the cube has unit size and is centered at the origin.

1  void draw() {
2    renderer.push();
3        renderer.translate(vec3(0.5, 0.5, 0.0));
4
5        renderer.push();
6            renderer.translate(vec3(-0.5, -0.5, 0.0));
7            renderer.scale(vec3(0.25));
8            renderer.cube();
9        renderer.pop();
10
11       renderer.scale(vec3(0.25));
12       renderer.sphere();
13   renderer.pop();
14  }

  • On line 8 of the following program, what are the contents of the matrix stack?

1  void draw() {
2    renderer.push();
3        renderer.translate(vec3(0.5, 0.5, 0.0));
4
5        renderer.push();
6            renderer.translate(vec3(-0.5, -0.5, 0.0));
7            renderer.scale(vec3(0.25));
8            renderer.cube();
9        renderer.pop();
10
11       renderer.scale(vec3(0.25));
12       renderer.sphere();
13   renderer.pop();
14  }

  • Draw the scene corresponding to the following code.

1  void draw() {
2    renderer.push();
3        renderer.translate(vec3(0.5, 0.5, 0.0));
4
5        renderer.push();
6            renderer.translate(vec3(-0.5, -0.5, 0.0));
7            renderer.scale(vec3(0.25));
8            renderer.cube();
9        renderer.pop();
10
11       renderer.scale(vec3(0.25));
12       renderer.sphere();
13   renderer.pop();
14  }

  • Sketch code for implementing a cone that always faces the camera.

  • Sketch an algorithm for implementing a particle system that implements a dust trail effect. How should particles be initialized? And how should they be updated?

  • Suppose I have an object with bounding box (5, 10, 1). How can I rescale the box so it fits inside a unit cube. Be cause that your approach does not distort the model!

  • Sketch the algorithm for implementing a car that drives in a circle. Orient the car so it faces the direction of travel.

  • Consider the following code. Modify it to place Beethoven at the steering wheel. Assume the steering wheel is offset by (5, 1, 1) from the local position of the car. Also scale Beethoven to be 10% of its original size. Assume that both the car and Beethoven have their origin centered at the base of the model.

  void draw() {

    float theta = elapsedTime();
    float px = radiusCar * cos(theta);
    float py = radiusCar * sin(theta);

    renderer.translate(vec3(px, py, 0.0));
    renderer.mesh(car);
  }

  • Consider the following texture. How would the texture appear on the each of the three shapes below?

texture

tex ex1

tex ex2

tex ex3

  • Suppose we shade the point p with the Phong shading model.

    • p = (0,3,1) with normal (0, sqrt(2)/2, sqrt(2)/2)

    • the camera is located at point e = (0,0,5) and has no rotation

    • the light is white and located at point el = (1,1,1)

    • the material of the object consists of (0.1, 0.1, 0.1) ambient lighting, (1,1,1) specular lighting with shininess 10, and (0,0,1) diffuse lighting

\[I = I_a + I_d + I_s, where\]
\[I_a = k_a M_a L_a\]
\[I_d = k_d M_d L_a (\hat{L} \cdot \hat{n})\]
\[I_s = k_s M_s L_s (\hat{v} \cdot \hat{r})^\alpha\]

Is p in light or shadow? Is p part of the specular hightlight, or no? Apply the phong shading equations to justify your answer.